La science du mouvement

La science du mouvement au XVIIe et XVIIIe siècles ou les fondements de la mécanique analytique

¹Massimo Corradi

¹Dipartimento di Scienze per l’Architettura, Scuola Politecnica - Genova, corradi@arch.unige.it

Introduction

Lagrange écrit dans l’Avertissement de sa Méchanique Analytique (Paris, 1788): «On a déjà plusieurs Traités de Méchanique, mais le plan de celui-ci est entièrement neuf. Je me suis proposé de réduire la théorie de cette science et l’art de résoudre les problèmes qui s’y rapportent, à des formules générales, dont le simple développement donne toutes les équations nécessaires pour la solution de chaque problème».

Cette «nouvelle vision du monde », qui sera celle du XVIIe siècle et encore plus celle du siècle suivant et qui tente d’établir un dialogue entre la Méchanique physique proposée par S.D. Poisson et la Mécanique analytique de Lagrange (reprise au XIXe siècle en termes plus précis par le courant des « axiomaticiens »), constitue un vaste et important projet scientifique qui dépasse les principes généraux de la Mécanique pour investir des lieux de recherche et des disciplines plus spécialisées et plus particulières comme, par exemple, la balistique et l’hydraulique.

Il s’agit d’une réévaluation de cette « philosophie de la nature » qui dépasse les frontières restreintes de la métaphysique - restée pendant des siècles à l’ombre de la pensée scholastique post médiévale - pour devenir une science de la réalité définie et absolue. Elle n’est donc plus une justification philosophique absolue de la réalité, mais une « axiomatisation » de la réalité physique en termes mathématiques. Ce qui donnera lieu à une recherche du formalisme pur, au développement de nouveaux instruments de type mathématique où la science est conçue comme un système hypothético-déductif, basé exclusivement sur un ensemble de définitions implicites formelles des entités fondamentales, choisies arbitrairement pourvu qu’elles soient compatibles avec la réalité naturelle.

Les arguments principaux qui ont leurs racines dans la mécanique analytique sont : 1) l’entrée en scène du nouveau calcul leibnizien et les grands débats de l’Académie Royale des Sciences de Paris (1684-1706) ; 2) quelques « prétextes » cinématiques concernent l’étude de la courbe isochrone, de la brachistochrone et de la courbe d’égale pression ; 3) le concept leibnizien de mouvement et son explication au moyen de l’algorithme de Varignon ; 4) le développement des explications de la science du mouvement : 4a) le mouvement des projectifs en milieu résistant, 4b) les premières études d’hydrodynamique. Nous nous limiterons ici pour des raisons de temps aux deux premiers points, réservant les deux autres pour une autre étude.

Géométrie, Axiomatique et Philosophie de la Nature

Leibniz, déjà, en introduisant ses «monades» comme «unités réelles» ou points matériels qui possèdent tant la «réalité» de l’atome (au mieux de la particule physique) que l’ « exactitude » du point mathématique (et donc l’immatérialité de l’entité même) avait ouvert la porte de cette nouvelle « conception » du monde. La recherche de « quelque chose » qui puisse être considérée comme première, suprême, universelle, absolue, nécessaire, éternelle, infinie, par opposition au fait ou à l’objet particulier, relatif, contingent, éphémère, fini, dérivé - en un mot ce qui étant soumis au devenir est destiné à finir - ou encore ce qui est ou est considéré comme immatériel, au-dessus du sensible, métaempirique, transcendant par opposition à ce qui est ou est considéré comme physique, naturel, matériel, empirique : cette nouvelle « philosophia naturalis » donne lieu à de nombreuses recherches et sujets d’étude à de nombreux savants pour chercher à - ou mieux tenter - de formuler cette nouvelle vision « mathématique » de la réalité de la nature.

La recherche d’un système d’axiomes - de vérités ou de principes que l’on puisse admettre sans discussions, principes certains par évidence immédiate et qui puisse constituer la base de nouvelles recherches [1] - en tant que « notions générales évidentes non démontrables », qui constituent le fondement de la Mécanique et qui donc pourraient donner une définition implicite des concepts et des entités fondamentales, constituait le défi lancé par Lagrange à la « Mécanique pratique » fille de la « Nouvelle science » d’origine galiléenne. Comme l’a écrit J. Merleau-Ponty dans sa préface au livre de M. Blay [2] « l’un des éléments les plus importants de la « révolution scientifique » du Grand Siècle fut l’inauguration du projet d’une science mathématique de la nature, se substituant à la physique qualitative héritée d’Aristote ».

Pour Descartes, comme pour Galilée, la géométrie n’était pas l’unique instrument ou mieux l’unique paradigme du vrai savoir. En fait, les concepts, les axiomes, les postulats de la Géométrie doivent permettre à la pensée humaine de pénétrer la nautre des choses, ou du moins de chercher à comprendre le langage à travers lequel Dieu a voulu s’exprimer, dans l’optique qui sera mise en évidence plus tard par Saint-Venant qui ira jusqu’à en faire l’objectif de sa recherche philosophique et scientifique [3].

Comme on peut le lire dans le « Manifeste du cercle de Vienne », la théorie physique n’est, au fond, rien d’autre qu’un système d’axiomes formels, plus ou moins conventionnels, associé à un ensemble de « définitions de coordination » qui assurent la correspondance entre les axiomes et les lois de la nature vérifiée par l’expérience. Donc la « Géométrie a perdu son rôle directeur et presque son identité épistémologique ». La mathématisation de pointe et sans préjugé, riche de principes, théorèmes, formalismes, langages a rendu les lois physiques de plus en plus incompréhensibles et a osé (ou en fait risque aujourd’hui) de ne plus faire comprendre de manière claire et univoque le sens des objectifs de ce projet scientifique. La qualité parfaite entre le tenseur de tension et celui des déformations, entités différentes qui décrivent des mondes et des caractéristiques physico-mathématiques et géométriques bien différentes, où l’unique différence réside uniquement dans la genèse du concept, dans la signification que l’on attribue au symbole, en est un excellent exemple.

L’invention de l’« algorithme » différentiel par Leibniz [4] qui permet de substituer l’application de règles de calcul originales, différentes du calcul numérique, à l’intuition géométrique, constitue le mélange qui donna naissance à la « nouveauté » de la mathématisation de la mécanique : « …l’algorithme précis d’un nouveau calcul qui permet de libérer l’imagination d’une attention continuelle aux figures… » [5]. En fait l’avantage offert par l’application du calcul différentiel fut bien compris par les géomètres contemporains de Leibniz plus portés à raisonner sur l’infiniment petit, même si des personnages comme Newton, les frères Bernoulli, l’Hospital et d’autres continueront à traiter les problèmes mécaniques, principalement ceux relatifs à la science du mouvement, en cherchant un équivalent géométrique au problème mathématique. En ce sens, dans le domaine de la science du mouvement, le calcul différentiel apparaissait comme un instrument auxiliaire de la géométrie. La synthèse audacieuse et géniale des Principia de Newton, développés en suivant une conception et une application purement géométriques des instruments mathématiques, encouragèrent de manière décisive les mathématiciens à rassembler leurs efforts pour rendre efficace les hypothèses de la science du mouvement et les principes mécaniques qui forment la base de cette « philosophie de la Nature » que nous avons évoquée.

Varignon, personnage secondaire dans le contexte de la fondation de la Mécanique analytique s’avèrera par contre, de première importance pour l’introduction du calcul différentiel dans la science du mouvement. Dans les travaux de Varignon, on ne trouve pas de manière claire et exhaustive, le concept de vitesse instantanée, mais sa définition du concept de « force accélératrice » (1698) lui permettra de jeter les bases d’une méthode générale de résolution des problèmes cinématiques de valeur incontestable, en éliminant de plus les différences entre les traitements mathématiques des quantités relatives au mouvement uniforme et au mouvement accéléré.

Dans cette perspective se situent les Principia de Newton [7] comme le texte de Huygens [8]. Dans ces deux textes on trouve, par rapport au traité galiléen [9], un développement considérable des sciences relatives à la Mécanique, mais dans ceux-ci l’utilisation de la mathématique, et en particulier ceux de la géométrie différentielle, est encore bien éloignée de celle des grands traités du XVIII^e siècle (cfr. d’Alembert, Lagrange, Laplace) où s’affirme avec force le prima du développement des procédures et des formalismes analytiques.

La publication dans les Acta Eruditorum dans les années 1684 et 1686 des mémoires de Leibniz sur le calcul différentiel entraîna une transformation conceptuelle profonde des mathématiques et par conséquent, une transformation particulièrement significative de la Mécanique à partir de la science du mouvement (par exemple la description de la trajectoire décrite sous certaines conditions, par les corps en mouvement). La détermination des trajectoires décrites par les corps en mouvement peut vraiment être le fruit d’une conceptualisation différentielle du problème mathématique ; c’est dans ce sens qui se pose le travail des frères Jacob et Johann Bernoulli lorsqu’en 1690, ils se fixent comme objectif de réduire le problème du mouvement à des problèmes de géométrie pure, susceptibles d’être résolus au moyen des nouveaux outils mathématiques. « La conceptualisation différentielle de la science du mouvement n’apparaît donc pas comme une conséquence immédiate de l’introduction du calcul leibnizien dans le champ du savoir » [10]. Les fondements mathématiques de cette nouvelle conceptualisation peuvent se trouver, par ailleurs, dans le traité de Fontenelle sur la Géométrie de l’infini [11].

On assiste donc à un changement important de paradigme où c’est l’étude de la mathématique qui conduit à développer de nouveaux problèmes appartenant au domaine des sciences mécaniques. En ce sens deux problèmes mécaniques intéressants, qui ouvriront deux disciplines aussi importantes que la ballistique et l’hydrodynamique, prendront une part importante de l’intérêt des scientifiques, qui pourront ainsi traiter les problèmes du mouvement relatif comme le mouvement des projectiles dans les milieux résistants et les premiers exercices d’hydrodynamique.

Breve excursus historique sur l'introduction du nouveau calcul Leibnizien

En 1684, Leibniz publie son traité Nova Methodus pro maximis et minimis [12], dans les Acta Eruditorum, où il donne une nouvelle méthode pour chercher les maximas et minimas ainsi que les tangentes d’une fonction donnée. Dans l’article suivant De geometria recondita et analysi indivisibilium atque infinitorum, Leibniz introduit le signe intégral (∫) – même si le mot « intégrale » ne fut introduit pour la première fois qu’en 1690 dans un texte écrit par Jacob Bernoulli [13] – entraînant un jugement favorable de Fontenelle [14] sur le travail qu’il a réalisé. Pourtant, le premier traité consacré au calcul leibnizien n’apparaît qu’en 1696, le Marquis Guillaume de l’Hospital, initié à cette nouvelle branche des mathématiques – le calcul différentiel et intégral – par les frères Bernoulli, publie sa célèbre Analyse des infiniment petits pour l’intelligence des lignes courbes. Il reste incontestable que le travail de Leibniz poursuit les réflexions mathématiques initiées par Descartes dans sa Géométrie publiée à Leyden en 1637. Leibniz souligne la très grande généralité de sa méthode ainsi que sa supériorité sur celles utilisées jusque là : voyez à ce sujet les algorithmes mathématiques proposés entre autres par Jean Hudde, Pierre Fermat, James Gregory, Isaac Barrow et John Wallis. « Lorsqu’on connaît l’algorithme, si je peux dire, de ce calcul que j’appelle différentiel…devait être fait avec les méthodes présentées jusqu’à ce jour » [15].

En dépit de le vaste horizon ouvert dans la mathématique par le calcul leibnizien, ses règles principales eurent une diffusion lente parmi les savants à cause, d’une part, du caractère novateur de cette méthode et, d’autre part, de l’extrême concision du texte leibnizien qui en rendait la lecture difficile. Un des premiers à apprécier le nouveau calcul fut Jacob Bernoulli [16]. Dans une note publiée en 1690 dans les Acta Eruditorum, Jacob Bernoulli résoud, au moyen du calcul différentiel, le problème de la courbe isochrone, problème proposé par Leibniz en 1687 [17], démontrant la puissance du nouvel instrument de calcul mais aussi l’élégance du traitement d’une question aussi difficile.

Dans les années qui suivirent 1690, les frères Jacob et Johann Bernoulli se consacrèrent avec énergie à l’application du nouveau calcul leibnizien aux sujets les plus variés de la géométrie, parmi lesquels l’étude des courbes élastiques qui aura de nombreuses applications théoriques dans la mécanique des structures [18].

Ensuite Varignon (1695) d’abord, Joseph Sauveur (1697) plus tard se consacreront à l’application du calcul leibnizien en utilisant comme instrument l’ Analyse des infiniment petits du Marquis de l’Hospital. Plus tard, encore, Thomas Fantet de Lagny (1696) et Philippe de La Hire (1697) se dédieront à ce sujet bien que ce dernier ait eu quelques doutes méthodologiques quant à l’éfficacité réelle de cette nouvelle méthode d’analyse. La critique de La Hire portait sur le fait qu’il est possible dans un cercle de confondre la corde et l’arc lorsque la grandeur de l’arc de circonférence est très petit, et donc – en se référant au théorème VI, proposition VII de la IIIe journée des Discorsi de Galileo – consacrée au mouvement d’un corps sur un plan incliné, de La Hire met en exergue l’erreur à laquelle on peut arriver et propose le problème de mécanique suivant : quelle est la courbe plane que doit parcourir une point massif à partir d’un point donné O, sans vitesse initiale, pour arriver à un autre point P dans le temps qu’il emploierait pour parcourir la corde OP De La Hire se propose alors de comparer l’arc et la corde « si l’on veut déterminer la différence du temps que le corps employé à parcourir l’arc DB, infiniment petit et sa corde, il ne sera pas difficile par la voye ordinaire… », comme d’ailleurs le montre Newton [19].

Comme l’on sait la solution de ce problème ou la courbe décrite n’est pas un arc de cercle mais une lemniscate de Bernoulli, ou un arc de lemniscate dont le centre est au point O et l’axe fait un angle de 45° avec l’horizontale [20].

Dès lors, de La Hire conseille de comparer les résultats obtenus par le calcul différentiel avec ceux déduits au moyen de la géométrie ordinaire, engendrant le jugement sévère de Leibniz qui l’accuse – dans une lettre à de l’Hospital – d’utiliser des méthodes « à la façon des Anciens » pour résoudre des problèmes tels que celui de l’épicycloïde [21]. L’usage de la « géométrie ordinaire » restait cependant, aux yeux de nombreux savants, l’unique instrument indispensable pour garantir l’exactitude des résultats obtenus. L’Abbé Bignon (président de l’Académie), le Père Gouye et l’Abbé Gallois, ainsi que Michel Rolle [22] resteront sur ces anciennes positions méthodologiques. Les critiques de Michel Rolle se basaient principalement sur deux arguments : 1) l’insuffisance et le manque de rigueur logique des concepts et des principes fondamentaux du nouveau calcul ; 2) le fait que le nouveau calcul conduisait à des résultats erronés ou pour le moins différents de ceux obtenus par les méthodes classiques [23].

Le prétexte cinématique

Sous le thème de prétexte cinématique nous rassemblons quelques considérations sur le problème de la détermination des trajectoires décrites, sous certaines conditions, par des corps en mouvement. Le point de départ de la discussion était l’étude des trajectoires décrites par les corps et fut l’enjeu de la querelle entre Leibniz et l’Abbé Catelan sur la « mesure des forces » ou autrement dit sur les forces vives. Le défi lancé par Leibniz aux cartésiens était le suivant : « trouver une ligne de descente, dans laquelle le corps pesant descende uniformément, et approche également de l’horizon en temps égaux », ou le problème de la ligne isochrone [24]. Il faut ici rappeler que les résultats de Galileo relatifs au mouvement rectiligne et uniforme et uniformément accéléré (décrits dans la IIIe journée des Discorsi) furent confirmés – donc le problème fut résolu sans faire appel au calcul différentiel – par Christiaan Huygens avec pour seul outil la géométrie infinitésimale classique. La démonstration de Huygens fait intervenir des grandeurs qui, si elles sont infinitésimales, sont évincées de la construction géométrique. En d’autres termes, son raisonnement ne fait pas appel à des formules algébriques mais seulement à des proportions entre segments géométriques [25].

La solution de Leibniz publiée dans « De Linea isochrona, in qua grave sive acceleratione descendit… » [26] montre en quoi sa solution est complémentaire de celle d’Huygens. Il est pourtant important de rappeler que la solution de Leibniz qualifiée de « très élégante » par ses contemporains – et même si l’auteur ne partage pas cet avis (« dépourvue d’élégance ») ne fait plus usage du calcul différentiel que celle de Huygens, il n’utilise pas le calcul différentiel. La solution de Jacob Bernoulli, qui paraît dans le numéro de mai des Acta Eruditorum, est par contre une solution plus « analytique ». Elle se compose de deux parties bien distinctes : une première partie qui a pour objectif de ramener le problème physique qui implique des considérations de mouvement à une pure question de géométrie (Unde problema, ad puram Geometriam reductum) [27] et une deuxième partie qui entend résoudre ce problème de géométrie à l’aide des concepts du calcul différentiel, obtenant comme solution la formule de la parabole semi-cubique. Johann Bernoulli s’applique au même problème et ses résultats furent publiés dans ses Lectiones Mathematicae [28]. Substantiellement identique au travail de son frère, celui de Johann est tout aussi intéressant par sa présentation plus didactique qui met mieux en évidence les hypothèses relatives à l’analyse du mouvement.

Durant ces mêmes années, d’autres problèmes de grand intérêt fascineront ceux qui étudient la mécanique et les nouveaux adeptes du calcul leibnizien : la courbe isochrone paracentrique, la courbe brachistochrone, la courbe d’égale pression, et d’autres thèmes importants de grande importance scientifique autre que mathématique.

Le premier problème consiste à définir la courbe isochrone paracentrique ou à déterminer la courbe le long de laquelle la chute d’un corps pesant est telle qu’il s’éloigne ou s’approche de manière uniforme à partir d’un point donné du point de chute. Ce problème fut proposé par Leibniz dans le numéro d’avril 1684 des Acta Eruditorum. Ce problème consiste à rechercher la courbe plane qu’un point pesant doit décrire pour que sa distance à un point fixe varie proportionnellement au temps nécessaire pour parcourir chaque arc de la courbe. Pour résoudre ce problème intéressant les plus grands savants de l’époque se mettent au travail parmi eux les frères Bernoulli et évidemment Leibniz. La première solution proposée publiquement au jugement des savants (elle paraît aux Acta Eruditorum de juin 1694) fut celle de Jacob Bernoulli, suivie immédiatement par la solution de Leibniz (publiée dans le numéro d’août de la même année dans les Acta Eruditorum), ensuite ce mémoire fit l’objet d’une réponse du même Bernoulli en septembre 1694. Une deuxième solution importante fut rendue publique toujours au même endroit par le frère de Jacob, Johann Bernoulli, au mois d’octobre 1694, témoignant d’un vif débat qui a eu lieu durant l’été 1694. Les deux solutions des frères Bernoulli sont très voisines tant dans leur style que dans leur esprit, même si celle de Johann Bernoulli est plus détaillée du point de vue du calcul leibnizien. La solution de Leibniz diffère par contre fortement de celle des frères Bernoulli. Sa solution adapte la même articulation du raisonnement qui caractérise l’étude de la courbe isochrone, ramenant la solution du problème à un problème de nature purement géométrique, mais susceptible d’être résolu par les méthodes du calcul différentiel ; dans la démonstration de Leibniz on met en évidence comment la construction de la courbe dépend en fait de la rectification d’un axe de lemniscate [29].

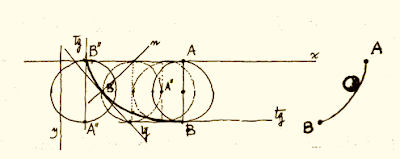
Le problème de la courbe brachistochrone, ou la recherche de la trajectoire qu’un point mobile soumis à une force déterminée doit décrire pour aller d’un point A à un point B dans le moins de temps possible (Fig. 1), fut proposé par contre par Johann Bernoulli dans le numéro de juin 1696 toujours des Acta Eruditorum, devenus le terrain sur lequel les plus grands savants de ce temps échangeaient leurs défis mathématiques. Le thème n’était certes pas neuf puisque Galileo l’avait abordé durant la IIIe journée des Discorsi (théorème XXII) même si pour lui la solution se ramenait simplement à un arc de cercle. Mais l’origine du thème comme formulé par Johann Bernoulli, avait des fins plus profondes où la mathématique et le nouveau calcul différentiel et intégral devaient fournir leurs réelles potentialités. Il était de plus dans les intentions de Bernoulli de mettre en évidence un problème important bien connu des géomètres, très utile en mécanique [30]. Par exemple, si nous examinons le problème d’un grave qui doit descendre, sans friction, d’un point A à un point B donné, on trouve que la brachistochrone est une cycloïde située dans le plan vertical passant par A et B (problème résolu par Johann Bernoulli en 1696 et qui est à l’origine des études sur le calcul des variations). Il était en fait connu, dans la construction des pendules à oscillations isochrones, que dans le cas où un point pesant se meut sans friction le long d’une cycloïde située dans un plan vertical, ce point atteind le point le plus bas dans le même temps quelque soit le point de la courbe dont il part (tautochronisme ou isochronisme). En fait, comme on le sait, la courbe tautochrone est la courbe située dans un plan vertical et ayant la propriété qu’un point pesant qui la parcourt avec ou sans friction, et éventuellement soumis de plus à une résistance du milieu proportioinnelle à la vitesse, atteind le point le plus bas (point de tautochronisme) toujours dans le même temps quelque soit la position de laquelle le point est livré à lui même à partir du repos ; d’éventuelles oscillations autour du point de tautochronisme ont une période indépendante de l’amplitude, et donc sont isochrones. On peut de plus démontrer que la courbe tautochrone est un arc de cycloïde ordinaire à base horizontale dont la concavité est tournée vers le haut.

Fig. 1 – Le problème de la courbe brachistochrone.

Le numéro de mai de l’année 1697 des Acta Eruditorum fut un numéro exceptionnel contenant la publication de quelques six solutions trouvées respectivement par Leibniz (pp. 201-205), Johann Bernoulli (pp. 206-211), Jacob Bernoulli (pp. 211-217), le Marquis de l’Hospital (pp. 217-218) [31], Tschirnhaus (pp. 220-223). Il faut préciser tout de suite que la solution de Tschirnhaus, basée sur l’hypothèse que la courbe est une cycloïde, est donnée sans aucune démonstration. Une solution, fut publiée anonymement, par Newton d’abord dans les Philosophical Transactions de 1697 [32], puis dans le même volume déjà mentionné des Acta Eruditorum.

Quelques remarques sur les solutions publiées. La solution de Leibniz part de l’hypothèse qui identifie la courbe à un polygone à un nombre infini de côtés. Chaque côté de longueur infinitésimale est tel qu’il est parcouru par un point massif en mouvement suivant les lois galiléennes du mouvement. Il associe, comme le fera d’ailleurs Jacob Bernoulli, les propriétés de la courbe valables en général à celles valables pour des quantités infinitésimales. Il faut souligner que Leibniz ramène le problème physique qui  implique la considération du mouvement à un problème de pure géométrie. La traduction en termes algébrico-différentiels des quantités géométriques conduit à la solution cherchée de l’équation différentielle de la cycloïde, courbe décrite par un point lié de manière rigide à un cercle (épicycle) qui roule dans le plan, sans glisser, sur une droite fixe. À chaque tour complet du cercle roulant correspond un « arc complet » de cycloïde. Ce qui confirme que la cycloïde est une courbe transcendante constituée d’une infinité d’arcs égaux entre eux. Il est important de rappeler que Leibniz, dans son mémoire, n’utilise pas ce terme qui lui sera suggéré par Johann Bernoulli dans une lettre du 21 juillet 1696 [33]. L’équation cherchée est la suivante:

dy/dx = √(x(2b-x)     (1)

La solution de Jacob Bernoulli part au contraire de l’hypothèse (lemme) que l’on peut remplacer le calcul du temps minimum nécessaire à parcourir la courbe entière par celui du temps minimum nécessaire à parcourir un arc infinitésimal. De cette manière on évite la difficulté liée au calcul de la différentielle d’une intégrale. La solution se développe de manière géométrique et mène pourtant à la même équation de la cycloïde. Jacob Bernoulli souligne, lui-même comme le fera son frère Johann, que ce problème dépasse la limite classique de la méthode des maximas et minimas, et requiert donc une autre approche mathématique.

Vice versa, la solution de Johann Bernoulli, bien qu’élégante du point de vue mathématique, a une portée plus limitée que celle de son frère Jacob. Il fait une analogie intéressante avec le problème de la réfraction d’un rayon lumineux, arrivant sous un certain angle d’incidence à travers un «milieu» optique formé par la superposition d’un nombre infini de strattes, tous homogènes entre eux mais dont la «densité» - au sens de l’opposition entre différentes raretés et caractérisant le «milieu» - varie le long de l’axe vertical. Un rayon lumineux émis par la source A se refracte à travers chacune des surfaces réfringentes qui séparent les strattes et se propage vers le point B suivant une certaine ligne courbe [34]. Cette ligne peut être assimilée à un polygone à un nombre infini de côtés rectilignes. Johann Bernoulli, utilisant les résultats de Fermat relatifs aux surfaces réfringentes déduit la courbe décrite par le rayon lumineux correspond, selon le principe de Fermat, à la trajectoire la plus rapide pour aller de A à B et donc la courbe brachistochrone cherchée. Il faut souligner que dans une telle analogie Johann Bernoulli n’utilise pas l’hypothèse de Galileo sur la chute des graves, mais considère une relation quelconque entre la vitesse et la hauteur de chute, qui exprime à travers une courbe arbitraire AHE. En conclusion, la brachistochrone et la cycloïde ordinaire où le cercle générateur de diamètre a roule sur le plan horizontal à partir d’un point fixe (donné). Ce que l’on formule de la manière suivante :

dy = dx√(x-(a-x)     (2)

Toujours est-il que, comme l’a écrit M. Blay : « Cette solution, bien que différente dans son principe des deux précédentes, ne fait pas intervenir, elle non plus, une quelconque conceptualisation différentielle de la science du mouvement » [35].

La solution de l’Hospital. Informé par Varignon du thème au centre des dissensions des plus grands savants de l’époque, au cours d’une correspondance suivie entre eux, l’Hospital, une fois le problème délivré des questions physiques et réduit à la « mathématique pure », se lance dans la solution du problème en s’inspirant du thème de la funiculaire et de la caténaire [36]. Dans son mémoire publié dans les Acta Eruditorum, inquiété aussi par quelques critiques de Johann Bernoulli visant son modus operandi l’Hospital n’expose que les résultats de son travail sans aucune démonstration. Dans une première version de sa démonstration l’Hospital se contente de montrer que la cycloïde, assimilée à un polygone à une infinité de côtés, vérifie la règle de proportionnalité établie entre le sinus de l’angle de la tangente à la courbe en un point et la verticale avec la vitesse de chute. Toujours est-il qu’il faut faire quelques observations et préciser pour mieux comprendre une telle solution. Soit AB=2r et r=1. La longueur de la demi-circonférence est alors égale à L=pr=p=3,14. Se rappelant que la tangente en un point de la cycloïde passe par l’extrémité du diamètre perpendiculaire à la droite sur laquelle roule le cercle générateur et que la normale à la tangente au point de contact passe par l’autre extrémité du diamètre du cercle générateur, on obtient, en termes galiléens, que la vitesse que le corps acquiert durant sa chute est directement proportionnelle à la racine carrée de la hauteur de chute. Sachant que les côtés du polygone qui approchent la courbe sont infinitésimaux et donc parcourus à une vitesse uniforme, on déduit que le corps va de B (voir Fig. 2) tournée de 90° à B’’ (de A en B), le long de la courbe AB dans un temps minimum, si cette courbe est une brachistochrone.

Fig.2 - Mouvement du corps pesant le long de la ligne AB.

La courbe d’égale pression. En avril 1695, dans un supplément aux Acta Eruditorum, Johann Bernoulli propose de déterminer la nature de la courbe d’égale pression (ou courbe centrifuge). Il s’agit de trouver, dans un plan vertical, la courbe décrite par un corps qui descend sous l’action de son poids propre alors qu’il est soumis à une pression en tous les points générée par une force constante égale à son poids. La solution du problème fut trouvée par Johann Bernoulli et communiquée à de l’Hospital après un long échange de lettres durant les années 1695-96 ; finalement cette solution fut mise au net par ce dernier et publiée en 1700 dans les Mémoires de l’Académie Royale des Sciences comme Solution d’un problème physico-mathématique.

Fig. 3a : Équilibre des forces; Fig. 3b : La courbe d’égale pression selon Johann Bernoulli

Le problème abordé par Johann Bernoulli est le suivant (Fig. 3b) : déterminer «la courbe EFM, dans laquelle le corps M descendant librement, et par sa propre pesanteur, la presse dans toutes ses parties avec une force égale à celle de son poids» ou, en utilisant à la manière de Huygens la développée HC de la courbe cherchée, « en sorte que le poids M attaché à l’extrémité d’un fil qui entoure cette développée, décrive en descendant cette ligne courbe ; il faut que dans chaque position du corps M, il tende le fil développée MC avec la même force que s’il étoit suspendu par ce fil» (Johann Bernoulli, 5 mars 1695). La solution du problème est beaucoup plus simple: il s’agit d’écrire que la somme des forces agissant suivant la normale à la trajectoire est constante et égale numériquement au poids. Il y a deux forces en jeu : la force centrifuge et la composante normale au poids. Il suffit alors d’écrire que la somme des intensités des deux forces est égale à celle du poids : mais – ajoute l’Hospital – le corps arrivé au point M tend le fil MC avec cette force centrifuge, augmentée de la partie de son poids qui agit sur le point M de cette courbe par l’effet de la pression suivant la perpendiculaire MS du poids «absolu» - c’est-à-dire la quantité MR. La solution est sans difficulté lorsque l’on sait « par les Mechaniques» que si l’on suppose que la partie constante MR de la verticale PM prolongée précisément de MR, exprime le poids absolu du corps M et que si nous traçons le segment RS perpendiculaire au segment MS qui coupe à angle droit la courbe au point M, alors la droite MS exprime la quantité avec laquelle le poids M agit sur le fil MC pour le tirer vers S. Le problème se réduit alors à déterminer l’intensité de la force centrifuge «avec laquelle ce corps tend le fil MC» exercé par le corps en mouvement, «afin de réduire cette question à la pure géométrie» [37].

Le calcul de la force centrifuge dans le cas du mouvement circulaire [38]. Quelques années plus tard, en 1687, Newton [39] donne la démonstration de ce problème dans le but de déterminer la force centripète. « Les corps qui parcourent uniformément différents cercles sont animés par des forces centripèdes qui tendent au centre de ces cercles, et qui sont entr’elles comme les quarrés des arcs décrits en temps égal, divisés par les rayons de ce cercle » [40]. La solution de l’Hospital, qui se fie à plusieurs reprises à Johann Bernoulli – déclarant ouvertement son « ignorance » de certaines questions physiques – est la suivante: « … la force centrifuge feroit parcourir au corps M, un espace égal au quarré de l’arc MN appliquée au diamètre MK, dans le même instant que ce corps parcoureroit l’arc MN ; puisque par le moyen de cette force, le corps M se trouvant en L au lieu d’être en N,  elle luy auroit fait parcourir la ligne NL» [41]. Cette affirmation de l’Hospital appelle une remarque : ce résultat qui permet, connaissant le rayon du cercle et la vitesse du mobile, d’exprimer le rapport d’une telle force centrifuge à d’autres, ne satisfait pas totalement des conditions du problème. Il est nécessaire, en fait, de mettre les deux forces en rapport avec un même terme de comparaison qualifié par Johann Bernoulli, de poids absolu. On comprend donc que l’Hospital désireux de trouver une solution correcte et exhaustive du problème, se tourne immédiatement vers la recherche de la solution d’un nouveau problème : déterminer la valeur du rapport des intensités des forces centrifuges au poids (ou gravité). En résumé, il s’agissait de comparer les espaces infiniment petits que, au même instant, la force centrifuge et la gravité font parcourir au même corps. L’hypothèse galiléenne du degré moyen [42] permet d’assimiler la vitesse constante du mobile M qui se meut sur un cercle de diamètre KM à celle générée par le même corps au cours d’une chute d’une hauteur égale à PM (Fig. 4).

Fig. 4 – Hypothèse galiléenne du «degré moyen».

Soit M le corps, t₁ le temps de chute de la hauteur PM, t₂ le temps de parcours de l’arc MN, alors on a:

 (t₁/t₂) = (2PM/MN) o (t₁²/t₂²) = (PM/(MN²/MN))

Donc la quantité (MN²)/(4PM) exprime l’espace que parcourerait le corps M au premier instant de la chute (durant lequel il parcourt l’arc MN). Il est donc possible de comparer « les espaces que font parcourir ces deux forces (la force centrifuge et la pesanteur) dans le même instant ». L’Hospital observe que l’on peut considérer la gravité comme une force qui agit uniformément et sans augmentation durant le premier instant de la chute à cause du caractère infinitésimal du temps écoulé [43].

Si l’on pose que, n est l’intensité de la vitesse de M sur le cercle de diamètre MK et g l’accélération de la pesanteur, alors la solution de l’Hospital conduit à la solution suivante. Appelons force centrifuge la quantité fc=((2PM/CM)•g), où g est la pesanteur (ou gravité), alors on peut écrire que cette force vaut fc=(v²/R). Cette équation représente l’expression de la force centrifuge dans le cas du mouvement circulaire uniforme. À présent, si CM=R, où R est le rayon de la circonférence, et (2PM)=(v²/g), avec g égale à l’accélération de la pesanteur on obtient le résultat cherché.

Dans le cas d’une trajectoire quelconque, si MR représente l’intensité de la pesanteur on obtient que la force centrifuge vaut fc=(2PM•MR)/MC, en chaque point de la trajectoire ou en chaque instant du mouvement. Cette trajectoire [44] peut être assimilée à une succession de petits arcs de cercle de rayon égal au rayon de courbure et où les centres décrivent la développée HC de la courbe EFM.

Le problème de la courbe d’égale pression se réduit donc à chercher une courbe EFM le long de laquelle l’expression (2PM•MR)/MC+MS = MR est toujours vérifiée. Le problème se réduit alors à un problème « de pure géométrie ». En substituant à chaque « élément » géométrique un symbole algébrique, par exemple MR=a, AP=x, PM=y, l’arce de courbe EFM=v, on obtient: MK=dx, Km=dy, Mm = dn (constant par l’hypothèse de l’uniformité du mouvement). En substituant et en simplifiant on peut écrire l’équation différentielle 2yddx+dydx=dvdy pour laquelle l’Hospital donne une solution [45]. Cette solution fit d’ailleurs l’objet en 1708 d’une querelle au sein de l’ l’Académie Royale des Sciences de Paris entre Parent et Saurin, due en substance à la difficulté de la nouvelle méthode de calcul utilisée. En tout cas la solution de l’Hospital fut reprise et développée des années plus tard (1710) par Varignon, avec rigueur de méthode, élégance du calcul et caractère complet de la présentation des solutions.

Conclusions

L’évolution de la recherche effectuée par les auteurs que nous avons cités se déroule principalement en deux étapes : 1) ramener les questions les plus importantes de la science du mouvement à des questions de «pure géométrie»; 2) résoudre ces questions de «pure géométrie» à l’aide des nouveaux « moyens » du calcul leibnizien. Cette évolution de la recherche basée sur de nouveaux principes et de nouveaux instruments mathématiques, contrairement à la finesse de certaines analyses de géométrie infinitésimale, d’inspiration newtonienne, appliquée au mouvement -  mais précisément exclusivement de géométrie infinitésimale à cause de la réduction effectuée dans la première étape – ne présente encore aucune conceptualisation différentielle spécifique de la science du mouvement susceptible d’être soumise à des procédures algorithmiques bien établies [46], puisque les grandes potentialités du calcul leibnizien sont encore à exprimer. La question restait donc encore ouverte mais les applications ultérieures au mouvement des projectiles dans un fluide élastique aux nouveaux principes de l’hydrodynamique par Daniel Bernoulli et à la mécanique des fluides en général, démontreront que les premières étapes de ce chemin nouveau et complexe de la mathématisation du monde physique donneront lieu à d’importantes modifications conceptuelles et linguistiques en Mécanique.

Bibliographie

[1] Kant E., Critica della ragion pura, a cura di Pietro Chiodi; trad. di Pietro Chiodi; Utet, Torino, 1967

[2] Merleau-Ponty J.: Préface. In: Blay M., La naissance de la mécanique analytique ; Puf, Paris, 1992, p. 3.

[3] Benvenuto, E.: Natural philosophy, rational mechanics and practical engineering in the work and life of Adhémar Jean Claude Barré de Saint-Venant, European Journal of Mechanics, A/Solids, vol. 16, Special issue, 1997, Gauthier-Villars, Paris, pp. 45-63. Vedi anche: Benvenuto, E.: Adhémar-Jean-Claude Barré de Saint-Venant: the Man, the Scientist, the Engineer, Atti dei convegni lincei, 140. Giornata lincea. Il problema di de Saint-Venant: aspetti teorici e applicativi (Roma, 6 marzo 1997), Accademia Nazionale dei Lincei, Roma, 1998, pp. 7-34.

[4] Leibniz, G.-W.: Nova methodus pro maximis et minimis, itemque tangentibus, quae nec Fractas nec Irrationales quantitates moratur, et singulare pro illis calculi genus, Acta Eruditorum, Leipzig, 1864, pp. 467-473; Leibniz, G.-W.: De geometria recondita et analysi indivisibilium infinitorum, Acta Eruditorum, Leipzig, 1686, pp. 292-300.

[5] Gerhardt, von G.I. Leibnizens mathematische Schriften, Bd. 1-7; Halle, Berlin, 1849-63, V, p. 393.

[6] Blay, M., La naissance de la mécanique analytique; Puf, Paris, 1992.

[7] Newton, I., Philosophiae Naturalis Principia Mathematicae; Londini, 1687.

[8] Huygens, C., Horologium Oscillatorium; Paris, 1673.

[9] Galilei, G., Discorsi e dimostrazioni matematiche intorno a due nuove scienze …; Leyden, 1638.

[10] Blay, M., La naissance de la mécanique analytique; Puf, Paris, 1992, p. 8.

[11] Fontenelle B, Le Bovier de, Elémens de la Géometrie de l’infini; Paris, 1727.

[12] Leibniz, G.-W.: Nova Methodus pro maximis et minimis, op. cit., 1684.

[13] L'utilisation du terme “calcul” et “calcul intégré” et a fait l'objet d'un long conflit entre les frères Jacques et Jean Bernoulli, qui a eu lieu sur les pages de la.Acta eruditorum.

[14] Fontenelle, B, Le Bovier de, in: Histoire de l’Académie Royale des Sciences avec les mémoires de Mathématiques et de Physique pour la même année. Tirés des registres de cette Académie. Année 1705 (1706), p. 141.

[15] Gerhardt, von G.I. Leibnizens mathematische Schriften, Bd. 1-7; Halle, Berlin, 1849-63, V, pp. 222-223.

[16] Montucla, J. F., Histoire des Mathématiques; Paris, an VII, II, p. 323 (Première édition du second volume: Paris, 1758).

[17] Gerhardt, von G.I. Leibnizens mathematische Schriften, Bd. 1-7; Halle, Berlin, 1849-63, V, cap. III, § 1.

[18] Benvenuto, E., La scienza delle costruzioni e il suo sviluppo storico; Sansoni, Firenze, 1981.

[19] Newton, I., Principes Mathématiques de la philosophie Naturelle; Paris, 1756-1759. Traduction française du marquis du Chastelet (nouvelle édition: Blanchard, Paris, 1966).

[20] Saladani, G., Compendio d’Analisi, Bologna, 1775, libro II, cap. XIII.

[21] Archives de l’Académie des Sciences de Paris. Registres manuscrits des procès-verbaux des séances de l’Académie royale des Sciences des Paris. Fol. 26, v°. Cfr aussi: Gerhardt, von G.I. Leibnizens mathematische Schriften, Bd. 1-7; Halle, Berlin, 1849-63, I, p. 276.

[22] Sur la critique de M. Rolle au débat sur la infinilment petits voir aussi: Blay, M., La naissance de la mécanique analytique; Puf, Paris, 1992, pp. 42-62.

[23] Voir par exemple les travaux de Jean Hudde (1633-1704).

[24] Le nom de «courbe isochrone" a été introduite par Leibniz dans sa mémoire en 1689 intitulé:De Linea isochrona, in qua grave sive acceleratione descendit, et de controversia cum Dn Abbate D.C., Acta Eruditorum (1689), pp. 195-198.

[25] Huygens, C.: Solution du problème proposé par M. L. dans les Nouvelles de la République des Lettres du mois de septembre 1687, Oeuvres complètes de Christiaan Huygens, 22 vol.; Société hollandaise des sciences, La Haye, 1888-1950, IX, pp. 224-226.

[26] Leibniz, G.-W, op. cit., Acta Eruditorum (1689), pp. 195-198.

[27] Jacobi Bernoulli Basileensisi, Opera, 2 vol.; Genève, 1744.

[28] Lectiones Mathematicae. Varia problemata Physico-Mechanica, eorumque solutiones. Inventio Curvae descensus aequalibis. In: Johannis Bernoulli ... Opera omnia tam antea sparsim edita, quam hactenus inedita, vol. 4; Lausanne et Genève, 1742.

[29] Della rettifica degli archi di una curva elastica, cfr. Jacobi Bernoulli Basileensisi, Opera, 2 vol.; Genève, 1744., vol. I, p. 603.

[30] Voir à cet égard Huygens, C., Horologium Oscillatorium; Paris, 1673, 2e partie et Newton, I. Philosophiae Naturalis Principia Mathematicae; Londini, 1687, Proposizione L.

[31] Une analyse approfondie de la mémoire des frères Bernoulli et le marquis de L'Hospital est situé dans J. Peiffer, J., Le problème de la brachystochrone à travers les relations de Jean I Bernoulli avec L’Hôpital et Varignon, Studia Leibnitiana, XVII (1989), pp. 59-81.

[32] Newton, I., Philosophical Transactions, Genn. 1697, pp. 384-389. Cet essai a été réédité en Acta Eruditorum, Maggio 1697, pp. 223-224.

[33] Gerhardt, von G.I. Leibnizens mathematische Schriften, Bd. 1-7; Halle, Berlin, 1849-63, II, pp. 298-299.

[34] Huygens, C., Traité de la lumière; Leyden, 1690, p. 46.

[35] Blay, M., La naissance de la mécanique analytique; Puf, Paris, 1992, p. 90.

[36] Voir le problème d'une corde lourde, souple, inextensible et homogène, suspendu à deux points fixes, le problème proposé par Jacques Bernoulli dans les mois de mai 1690 et réglé par Leibniz, Jean Bernoulli et Huygens. In: Benvenuto, E. op. cit.; Sansoni, Firenze, 1981.

[37] Histoire de l’Académie Royale des Sciences avec les Mémoires de Mathématiques et de Physique pour la même année. Tirés des registres de cette Académie. Année 1700 (1703), p. 10.

[38] Cfr. Huygens, C., Horologium Oscillatorium; Paris, 1673 (Parte 5a), Théorème I, II, III a pag. 102. Voir aussi le mémoire de 1659 intitulé «De vi centrifuga» publié à titre posthume en 1703 Volder et Fullenius, in Oeuvres complètes de Christiaan Huygens, 22 vol.; Société hollandaise des sciences, La Haye, 1888-1950. Opuscula Posthuma, XVI, pp. 260-267.

[39] Newton, I., Philosophiae Naturalis Principia Mathematicae; Londini, 1687, prop. IV, Sec. II, Libro I.

[40] Newton, I., Principes Mathématiques de la philosophie Naturelle; Paris, 1756-1759, p. 54, p. 56.

[41] L’Hospital, Marquis Guillaume de, Mém. Acad. Roy. Sci. Année 1700 (1703), p. 11.

[42] Galileo a montré que si un corps M se déplace  uniformément avec la vitesse qui acquiert une chute de hauteur PM, il se rendra dans le même temps une double ligne de PM. Voir Galilei, G., discours ..., op. Théorème cit., 3e jour, I, Proposition I.

[43] L’Hospital, Marquis Guillaume de,  Mém. Acad. Roy. Sci. Année 1700 (1703), pp. 11-12.

[44] L’Hospital, Marquis Guillaume de, Analyse des Infiniment petits pour l’intelligence des lignes courbes, Paris, 1696, e anche Jean Bernoulli, Lectiones Mathematicae. In: Opera omnia, Lausanne et Gèneve, 1742.

[45] L’Hospital, Marquis Guillaume de, Mém. Acad. Roy. Sci. Année 1700 (1703), p. 13.

[46] Blay, M., La naissance de la mécanique analytique; Puf, Paris, 1992, p. 109.