Introduction
Lagrange écrit dans l’Avertissement de sa Méchanique Analytique (Paris, 1788): «On a déjà plusieurs Traités de Méchanique, mais le plan de celui-ci est
entièrement neuf. Je me suis proposé de réduire la théorie de cette science et
l’art de résoudre les problèmes qui s’y rapportent, à des formules générales,
dont le simple développement donne toutes les équations nécessaires pour la
solution de chaque problème».
Cette «nouvelle vision du monde », qui sera celle du XVIIe siècle
et encore plus celle du siècle suivant et qui tente d’établir un dialogue entre
la Méchanique physique proposée par
S.D. Poisson et la Mécanique analytique
de Lagrange (reprise au XIXe siècle en termes plus précis par le courant des
« axiomaticiens »), constitue un vaste et important projet
scientifique qui dépasse les principes généraux de la Mécanique pour investir
des lieux de recherche et des disciplines plus spécialisées et plus
particulières comme, par exemple, la balistique et l’hydraulique.
Il s’agit d’une réévaluation de cette « philosophie de la
nature » qui dépasse les frontières restreintes de la métaphysique -
restée pendant des siècles à l’ombre de la pensée scholastique post médiévale -
pour devenir une science de la réalité définie et absolue. Elle n’est donc plus
une justification philosophique absolue de la réalité, mais une « axiomatisation »
de la réalité physique en termes mathématiques. Ce qui donnera lieu à une
recherche du formalisme pur, au développement de nouveaux instruments de type
mathématique où la science est conçue comme un système hypothético-déductif,
basé exclusivement sur un ensemble de définitions implicites formelles des
entités fondamentales, choisies arbitrairement pourvu qu’elles soient
compatibles avec la réalité naturelle.
Les arguments principaux qui ont leurs racines dans la mécanique
analytique sont : 1) l’entrée en scène du nouveau calcul leibnizien et les
grands débats de l’Académie Royale des
Sciences de Paris (1684-1706) ; 2) quelques « prétextes »
cinématiques concernent l’étude de la courbe isochrone, de la brachistochrone
et de la courbe d’égale pression ; 3) le concept leibnizien de mouvement
et son explication au moyen de l’algorithme de Varignon ; 4) le
développement des explications de la science du mouvement : 4a) le
mouvement des projectifs en milieu résistant, 4b) les premières études d’hydrodynamique.
Nous nous limiterons ici pour des raisons de temps aux deux premiers points,
réservant les deux autres pour une autre étude.
Géométrie,
Axiomatique et Philosophie de la Nature
Leibniz, déjà, en introduisant ses «monades»
comme «unités réelles» ou points matériels qui possèdent tant la «réalité» de
l’atome (au mieux de la particule physique) que l’ « exactitude » du
point mathématique (et donc l’immatérialité de l’entité même) avait ouvert la
porte de cette nouvelle « conception » du monde. La recherche de
« quelque chose » qui puisse être considérée comme première, suprême,
universelle, absolue, nécessaire, éternelle, infinie, par opposition au fait ou
à l’objet particulier, relatif, contingent, éphémère, fini, dérivé - en un mot
ce qui étant soumis au devenir est destiné à finir - ou encore ce qui est ou
est considéré comme immatériel, au-dessus du sensible, métaempirique,
transcendant par opposition à ce qui est ou est considéré comme physique,
naturel, matériel, empirique : cette nouvelle « philosophia
naturalis » donne lieu à de nombreuses recherches et sujets d’étude à de
nombreux savants pour chercher à - ou
mieux tenter - de formuler cette nouvelle vision « mathématique » de
la réalité de la nature.
La recherche d’un système d’axiomes - de vérités ou de principes que
l’on puisse admettre sans discussions, principes certains par évidence
immédiate et qui puisse constituer la base de nouvelles recherches [1] - en
tant que « notions générales évidentes non démontrables », qui constituent
le fondement de la Mécanique et qui donc pourraient donner une définition
implicite des concepts et des entités fondamentales, constituait le défi lancé
par Lagrange à la « Mécanique pratique » fille de la « Nouvelle
science » d’origine galiléenne. Comme l’a écrit J. Merleau-Ponty dans sa
préface au livre de M. Blay [2] « l’un
des éléments les plus importants de la « révolution scientifique » du
Grand Siècle fut l’inauguration du projet d’une science mathématique de la
nature, se substituant à la physique qualitative héritée d’Aristote ».
Pour Descartes, comme pour Galilée, la géométrie n’était pas l’unique
instrument ou mieux l’unique paradigme du vrai savoir. En fait, les concepts,
les axiomes, les postulats de la Géométrie doivent permettre à la pensée humaine
de pénétrer la nautre des choses, ou du moins de chercher à comprendre le
langage à travers lequel Dieu a voulu s’exprimer, dans l’optique qui sera mise
en évidence plus tard par Saint-Venant qui ira jusqu’à en faire l’objectif de
sa recherche philosophique et scientifique [3].
Comme on peut le lire dans le « Manifeste du cercle de
Vienne », la théorie physique n’est, au fond, rien d’autre qu’un système
d’axiomes formels, plus ou moins conventionnels, associé à un ensemble de
« définitions de coordination »
qui assurent la correspondance entre les axiomes et les lois de la nature
vérifiée par l’expérience. Donc la « Géométrie
a perdu son rôle directeur et presque son identité épistémologique ».
La mathématisation de pointe et sans préjugé, riche de principes, théorèmes,
formalismes, langages a rendu les lois physiques de plus en plus
incompréhensibles et a osé (ou en fait risque aujourd’hui) de ne plus faire
comprendre de manière claire et univoque le sens des objectifs de ce projet
scientifique. La qualité parfaite entre le tenseur de tension et celui des
déformations, entités différentes qui décrivent des mondes et des
caractéristiques physico-mathématiques et géométriques bien différentes, où
l’unique différence réside uniquement dans la genèse du concept, dans la
signification que l’on attribue au symbole, en est un excellent exemple.
L’invention de
l’« algorithme » différentiel par Leibniz [4] qui permet de
substituer l’application de règles de calcul originales, différentes du calcul
numérique, à l’intuition géométrique, constitue le mélange qui donna naissance
à la « nouveauté » de la mathématisation de la mécanique :
« …l’algorithme précis d’un nouveau
calcul qui permet de libérer l’imagination d’une attention continuelle aux
figures… » [5]. En fait l’avantage offert par l’application du calcul
différentiel fut bien compris par les géomètres contemporains de Leibniz plus
portés à raisonner sur l’infiniment petit, même si des personnages comme
Newton, les frères Bernoulli, l’Hospital et d’autres continueront à traiter les
problèmes mécaniques, principalement ceux relatifs à la science du mouvement,
en cherchant un équivalent géométrique au problème mathématique. En ce sens,
dans le domaine de la science du mouvement, le calcul différentiel apparaissait
comme un instrument auxiliaire de la géométrie. La synthèse audacieuse et
géniale des Principia de Newton,
développés en suivant une conception et une application purement géométriques
des instruments mathématiques, encouragèrent de manière décisive les
mathématiciens à rassembler leurs efforts pour rendre efficace les hypothèses
de la science du mouvement et les principes mécaniques qui forment la base de
cette « philosophie de la Nature » que nous avons évoquée.
Varignon, personnage secondaire
dans le contexte de la fondation de la Mécanique
analytique s’avèrera par contre, de première importance pour l’introduction
du calcul différentiel dans la science du mouvement. Dans les travaux de
Varignon, on ne trouve pas de manière claire et exhaustive, le concept de
vitesse instantanée, mais sa définition du concept de « force
accélératrice » (1698) lui permettra de jeter les bases d’une méthode
générale de résolution des problèmes cinématiques de valeur incontestable, en
éliminant de plus les différences entre les traitements mathématiques des
quantités relatives au mouvement uniforme et au mouvement accéléré.
Dans cette perspective se
situent les Principia de Newton [7]
comme le texte de Huygens [8]. Dans ces deux textes on trouve, par rapport au
traité galiléen [9], un développement considérable des sciences relatives à la
Mécanique, mais dans ceux-ci l’utilisation de la mathématique, et en
particulier ceux de la géométrie différentielle, est encore bien éloignée de
celle des grands traités du XVIIIe siècle (cfr. d’Alembert,
Lagrange, Laplace) où s’affirme avec force le prima du développement des
procédures et des formalismes analytiques.
La publication dans les Acta Eruditorum dans les années 1684 et
1686 des mémoires de Leibniz sur le calcul différentiel entraîna une
transformation conceptuelle profonde des mathématiques et par conséquent, une
transformation particulièrement significative de la Mécanique à partir de la
science du mouvement (par exemple la description de la trajectoire décrite sous
certaines conditions, par les corps en mouvement). La détermination des
trajectoires décrites par les corps en mouvement peut vraiment être le fruit
d’une conceptualisation différentielle du problème mathématique ; c’est
dans ce sens qui se pose le travail des frères Jacob et Johann Bernoulli
lorsqu’en 1690, ils se fixent comme objectif de réduire le problème du
mouvement à des problèmes de géométrie pure, susceptibles d’être résolus au
moyen des nouveaux outils mathématiques. « La conceptualisation différentielle de la science du mouvement
n’apparaît donc pas comme une conséquence immédiate de l’introduction du calcul
leibnizien dans le champ du savoir » [10]. Les fondements
mathématiques de cette nouvelle conceptualisation peuvent se trouver, par
ailleurs, dans le traité de Fontenelle sur la Géométrie de l’infini [11].
On assiste donc à un changement
important de paradigme où c’est l’étude de la mathématique qui conduit à
développer de nouveaux problèmes appartenant au domaine des sciences
mécaniques. En ce sens deux problèmes mécaniques intéressants, qui ouvriront
deux disciplines aussi importantes que la ballistique et l’hydrodynamique,
prendront une part importante de l’intérêt des scientifiques, qui pourront
ainsi traiter les problèmes du mouvement relatif comme le mouvement des projectiles dans les milieux résistants et les
premiers exercices d’hydrodynamique.
Breve excursus historique sur l'introduction du nouveau calcul Leibnizien
En 1684, Leibniz publie son
traité Nova Methodus pro maximis et
minimis [12], dans les Acta
Eruditorum, où il donne une nouvelle méthode pour chercher les maximas et
minimas ainsi que les tangentes d’une fonction donnée. Dans l’article suivant De geometria recondita et analysi
indivisibilium atque infinitorum, Leibniz introduit le signe intégral (∫) –
même si le mot « intégrale » ne fut introduit pour la première fois
qu’en 1690 dans un texte écrit par Jacob Bernoulli [13] – entraînant un
jugement favorable de Fontenelle [14] sur le travail qu’il a réalisé. Pourtant,
le premier traité consacré au calcul leibnizien n’apparaît qu’en 1696, le
Marquis Guillaume de l’Hospital, initié à cette nouvelle branche des
mathématiques – le calcul différentiel et intégral – par les frères Bernoulli,
publie sa célèbre Analyse des infiniment
petits pour l’intelligence des lignes courbes. Il reste incontestable que
le travail de Leibniz poursuit les réflexions mathématiques initiées par
Descartes dans sa Géométrie publiée à
Leyden en 1637. Leibniz souligne la très grande généralité de sa méthode ainsi
que sa supériorité sur celles utilisées jusque là : voyez à ce sujet les
algorithmes mathématiques proposés entre autres par Jean Hudde, Pierre Fermat,
James Gregory, Isaac Barrow et John Wallis. « Lorsqu’on connaît l’algorithme, si je peux dire, de ce calcul que
j’appelle différentiel…devait être fait avec les méthodes présentées jusqu’à ce
jour » [15].
En dépit de le vaste horizon
ouvert dans la mathématique par le calcul leibnizien, ses règles principales
eurent une diffusion lente parmi les savants à cause, d’une part, du caractère
novateur de cette méthode et, d’autre part, de l’extrême concision du texte
leibnizien qui en rendait la lecture difficile. Un des premiers à apprécier le
nouveau calcul fut Jacob Bernoulli [16]. Dans une note publiée en 1690 dans les
Acta Eruditorum, Jacob Bernoulli
résoud, au moyen du calcul différentiel, le problème de la courbe isochrone,
problème proposé par Leibniz en 1687 [17], démontrant la puissance du nouvel
instrument de calcul mais aussi l’élégance du traitement d’une question aussi
difficile.
Dans les années qui suivirent
1690, les frères Jacob et Johann Bernoulli se consacrèrent avec énergie à
l’application du nouveau calcul leibnizien aux sujets les plus variés de la
géométrie, parmi lesquels l’étude des courbes élastiques qui aura de nombreuses
applications théoriques dans la mécanique des structures [18].
Ensuite Varignon (1695)
d’abord, Joseph Sauveur (1697) plus tard se consacreront à l’application du
calcul leibnizien en utilisant comme instrument l’ Analyse des infiniment petits du Marquis de l’Hospital. Plus tard,
encore, Thomas Fantet de Lagny (1696) et Philippe de La Hire (1697) se
dédieront à ce sujet bien que ce dernier ait eu quelques doutes méthodologiques
quant à l’éfficacité réelle de cette nouvelle méthode d’analyse. La critique de
La Hire portait sur le fait qu’il est possible dans un cercle de confondre la
corde et l’arc lorsque la grandeur de l’arc de circonférence est très petit, et
donc – en se référant au théorème VI, proposition VII de la IIIe journée des Discorsi de Galileo – consacrée au
mouvement d’un corps sur un plan incliné, de La Hire met en exergue l’erreur à
laquelle on peut arriver et propose le problème de mécanique suivant :
quelle est la courbe plane que doit parcourir une point massif à partir d’un
point donné O, sans vitesse initiale,
pour arriver à un autre point P dans
le temps qu’il emploierait pour parcourir la corde OP De La Hire se propose alors de comparer l’arc et la corde
« si l’on veut déterminer la
différence du temps que le corps employé à parcourir l’arc DB, infiniment petit et sa corde, il ne sera
pas difficile par la voye ordinaire… », comme d’ailleurs le montre
Newton [19].
Comme l’on sait la solution de
ce problème ou la courbe décrite n’est pas un arc de cercle mais une lemniscate
de Bernoulli, ou un arc de lemniscate dont le centre est au point O et l’axe fait un angle de 45° avec
l’horizontale [20].
Dès lors, de La Hire conseille
de comparer les résultats obtenus par le calcul différentiel avec ceux déduits
au moyen de la géométrie ordinaire, engendrant le jugement sévère de Leibniz
qui l’accuse – dans une lettre à de l’Hospital – d’utiliser des méthodes « à la façon des Anciens »
pour résoudre des problèmes tels que celui de l’épicycloïde [21]. L’usage de la
« géométrie ordinaire »
restait cependant, aux yeux de nombreux savants, l’unique instrument
indispensable pour garantir l’exactitude des résultats obtenus. L’Abbé Bignon
(président de l’Académie), le Père
Gouye et l’Abbé Gallois, ainsi que Michel Rolle [22] resteront sur ces
anciennes positions méthodologiques. Les critiques de Michel Rolle se basaient
principalement sur deux arguments : 1) l’insuffisance et le manque de
rigueur logique des concepts et des principes fondamentaux du nouveau
calcul ; 2) le fait que le nouveau calcul conduisait à des résultats
erronés ou pour le moins différents de ceux obtenus par les méthodes classiques
[23].
Le prétexte cinématique
Sous le thème de prétexte cinématique nous rassemblons quelques considérations sur
le problème de la détermination des trajectoires décrites, sous certaines
conditions, par des corps en mouvement. Le point de départ de la discussion
était l’étude des trajectoires décrites par les corps et fut l’enjeu de la querelle entre Leibniz et l’Abbé Catelan
sur la « mesure des forces »
ou autrement dit sur les forces vives. Le défi lancé par Leibniz aux cartésiens
était le suivant : « trouver
une ligne de descente, dans laquelle le corps pesant descende uniformément, et
approche également de l’horizon en temps égaux », ou le problème de la
ligne isochrone [24]. Il faut ici rappeler que les résultats de Galileo
relatifs au mouvement rectiligne et uniforme et uniformément accéléré (décrits
dans la IIIe journée des Discorsi)
furent confirmés – donc le problème fut résolu sans faire appel au calcul
différentiel – par Christiaan Huygens avec pour seul outil la géométrie
infinitésimale classique. La démonstration de Huygens fait intervenir des
grandeurs qui, si elles sont infinitésimales, sont évincées de la
construction géométrique. En d’autres termes, son raisonnement ne fait pas
appel à des formules algébriques mais seulement à des proportions entre
segments géométriques [25].
La solution de Leibniz publiée
dans « De Linea isochrona, in qua
grave sive acceleratione descendit… » [26] montre en quoi sa solution
est complémentaire de celle d’Huygens. Il est pourtant important de rappeler
que la solution de Leibniz qualifiée de « très
élégante » par ses contemporains – et même si l’auteur ne partage pas
cet avis (« dépourvue d’élégance »)
ne fait plus usage du calcul différentiel que celle de Huygens, il n’utilise
pas le calcul différentiel. La solution de Jacob Bernoulli, qui paraît dans le
numéro de mai des Acta Eruditorum,
est par contre une solution plus « analytique ».
Elle se compose de deux parties bien distinctes : une première partie qui
a pour objectif de ramener le problème physique qui implique des considérations
de mouvement à une pure question de géométrie (Unde problema, ad puram Geometriam reductum) [27] et une deuxième
partie qui entend résoudre ce problème de géométrie à l’aide des concepts du
calcul différentiel, obtenant comme solution la formule de la parabole
semi-cubique. Johann Bernoulli s’applique au même problème et ses résultats
furent publiés dans ses Lectiones
Mathematicae [28]. Substantiellement identique au travail de son frère,
celui de Johann est tout aussi intéressant par sa présentation plus didactique
qui met mieux en évidence les hypothèses relatives à l’analyse du mouvement.
Durant ces mêmes années,
d’autres problèmes de grand intérêt fascineront ceux qui étudient la mécanique
et les nouveaux adeptes du calcul leibnizien : la courbe isochrone paracentrique, la courbe brachistochrone, la courbe
d’égale pression, et d’autres thèmes importants de grande importance
scientifique autre que mathématique.
Le premier problème consiste à
définir la courbe isochrone paracentrique ou à déterminer la courbe le long de
laquelle la chute d’un corps pesant est telle qu’il s’éloigne ou s’approche de
manière uniforme à partir d’un point donné du point de chute. Ce problème fut
proposé par Leibniz dans le numéro d’avril 1684 des Acta Eruditorum. Ce problème consiste à rechercher la courbe plane
qu’un point pesant doit décrire pour que sa distance à un point fixe varie
proportionnellement au temps nécessaire pour parcourir chaque arc de la courbe.
Pour résoudre ce problème intéressant les plus grands savants de l’époque se
mettent au travail parmi eux les frères Bernoulli et évidemment Leibniz. La
première solution proposée publiquement au jugement des savants (elle paraît
aux Acta Eruditorum de juin 1694) fut
celle de Jacob Bernoulli, suivie immédiatement par la solution de Leibniz
(publiée dans le numéro d’août de la même année dans les Acta Eruditorum), ensuite ce mémoire fit l’objet d’une réponse du
même Bernoulli en septembre 1694. Une deuxième solution importante fut rendue
publique toujours au même endroit par le frère de Jacob, Johann Bernoulli, au
mois d’octobre 1694, témoignant d’un vif débat qui a eu lieu durant l’été 1694.
Les deux solutions des frères Bernoulli sont très voisines tant dans leur style
que dans leur esprit, même si celle de Johann Bernoulli est plus détaillée du
point de vue du calcul leibnizien. La solution de Leibniz diffère par contre
fortement de celle des frères Bernoulli. Sa solution adapte la même
articulation du raisonnement qui caractérise l’étude de la courbe isochrone,
ramenant la solution du problème à un problème de nature purement géométrique,
mais susceptible d’être résolu par les méthodes du calcul différentiel ;
dans la démonstration de Leibniz on met en évidence comment la construction de
la courbe dépend en fait de la rectification d’un axe de lemniscate [29].
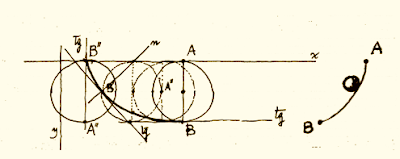
Le problème de la courbe brachistochrone, ou la recherche
de la trajectoire qu’un point mobile soumis à une force déterminée doit décrire
pour aller d’un point A à un point B dans le moins de temps possible (Fig.
1), fut proposé par contre par Johann Bernoulli dans le numéro de juin 1696
toujours des Acta Eruditorum, devenus
le terrain sur lequel les plus grands savants de ce temps échangeaient leurs
défis mathématiques. Le thème n’était certes pas neuf puisque Galileo l’avait
abordé durant la IIIe journée des Discorsi
(théorème XXII) même si pour lui la solution se ramenait simplement à un arc de
cercle. Mais l’origine du thème comme formulé par Johann Bernoulli, avait
des fins plus profondes où la mathématique et le nouveau calcul différentiel et
intégral devaient fournir leurs réelles potentialités. Il était de plus dans
les intentions de Bernoulli de mettre en évidence un problème important bien
connu des géomètres, très utile en mécanique [30]. Par exemple, si nous
examinons le problème d’un grave qui doit descendre, sans friction, d’un point A à un point B donné, on trouve que la brachistochrone
est une cycloïde située dans le plan vertical passant par A et B (problème résolu
par Johann Bernoulli en 1696 et qui est à l’origine des études sur le calcul
des variations). Il était en fait connu, dans la construction des pendules à
oscillations isochrones, que dans le cas où un point pesant se meut sans
friction le long d’une cycloïde située dans un plan vertical, ce point atteind
le point le plus bas dans le même temps quelque soit le point de la courbe dont
il part (tautochronisme ou isochronisme). En fait, comme on le
sait, la courbe tautochrone est la
courbe située dans un plan vertical et ayant la propriété qu’un point pesant
qui la parcourt avec ou sans friction, et éventuellement soumis de plus à une
résistance du milieu proportioinnelle à la vitesse, atteind le point le plus
bas (point de tautochronisme)
toujours dans le même temps quelque soit la position de laquelle le point est
livré à lui même à partir du repos ; d’éventuelles oscillations autour du
point de tautochronisme ont une période indépendante de l’amplitude, et donc
sont isochrones. On peut de plus démontrer que la courbe tautochrone est un arc de cycloïde ordinaire à base horizontale
dont la concavité est tournée vers le haut.
Fig. 1 – Le problème de la courbe brachistochrone.
Le numéro de mai de l’année 1697 des Acta Eruditorum fut un numéro
exceptionnel contenant la publication de quelques six solutions trouvées respectivement par Leibniz (pp. 201-205),
Johann Bernoulli (pp. 206-211), Jacob Bernoulli (pp. 211-217), le Marquis de
l’Hospital (pp. 217-218) [31], Tschirnhaus (pp. 220-223). Il faut préciser tout
de suite que la solution de Tschirnhaus, basée sur l’hypothèse que la courbe
est une cycloïde, est donnée sans aucune démonstration. Une solution, fut
publiée anonymement, par Newton d’abord dans les Philosophical Transactions de 1697 [32], puis dans le même volume
déjà mentionné des Acta Eruditorum.
Quelques remarques sur les solutions publiées. La solution de Leibniz part de l’hypothèse
qui identifie la courbe à un polygone à un nombre infini de côtés. Chaque côté
de longueur infinitésimale est tel qu’il est parcouru par un point massif en
mouvement suivant les lois galiléennes du mouvement. Il associe, comme le fera
d’ailleurs Jacob Bernoulli, les propriétés de la courbe valables en général à
celles valables pour des quantités infinitésimales. Il faut souligner que
Leibniz ramène le problème physique qui
implique la considération du mouvement à un problème de pure géométrie.
La traduction en termes algébrico-différentiels des quantités géométriques
conduit à la solution cherchée de l’équation différentielle de la cycloïde,
courbe décrite par un point lié de manière rigide à un cercle (épicycle) qui
roule dans le plan, sans glisser, sur une droite fixe. À chaque tour complet du
cercle roulant correspond un « arc complet » de cycloïde. Ce qui
confirme que la cycloïde est une courbe transcendante constituée d’une infinité
d’arcs égaux entre eux. Il est important de rappeler que Leibniz, dans son
mémoire, n’utilise pas ce terme qui lui sera suggéré par Johann Bernoulli dans
une lettre du 21 juillet 1696 [33]. L’équation cherchée est la suivante:
dy/dx = √(x(2b-x) (1)
La solution de Jacob Bernoulli
part au contraire de l’hypothèse (lemme) que l’on peut remplacer le calcul du
temps minimum nécessaire à parcourir la courbe entière par celui du temps
minimum nécessaire à parcourir un arc infinitésimal. De cette manière on évite
la difficulté liée au calcul de la différentielle d’une intégrale. La solution
se développe de manière géométrique et mène pourtant à la même équation de la
cycloïde. Jacob Bernoulli souligne, lui-même comme le fera son frère Johann,
que ce problème dépasse la limite classique de la méthode des maximas et
minimas, et requiert donc une autre approche mathématique.
Vice
versa, la solution de Johann Bernoulli, bien qu’élégante du point de vue
mathématique, a une portée plus limitée que celle de son frère Jacob. Il fait
une analogie intéressante avec le problème de la réfraction d’un rayon
lumineux, arrivant sous un certain angle d’incidence à travers un «milieu»
optique formé par la superposition d’un nombre infini de strattes, tous homogènes
entre eux mais dont la «densité» - au sens de l’opposition entre différentes
raretés et caractérisant le «milieu» - varie le long de l’axe vertical. Un
rayon lumineux émis par la source A
se refracte à travers chacune des surfaces réfringentes qui séparent les
strattes et se propage vers le point B
suivant une certaine ligne courbe [34]. Cette ligne peut être assimilée à un
polygone à un nombre infini de côtés rectilignes. Johann Bernoulli, utilisant
les résultats de Fermat relatifs aux surfaces réfringentes déduit la courbe
décrite par le rayon lumineux correspond, selon le principe de Fermat, à la
trajectoire la plus rapide pour aller de A
à B et donc la courbe brachistochrone
cherchée. Il faut souligner que dans une telle analogie Johann Bernoulli
n’utilise pas l’hypothèse de Galileo sur la chute des graves, mais considère
une relation quelconque entre la vitesse et la hauteur de chute, qui exprime à
travers une courbe arbitraire AHE. En
conclusion, la brachistochrone et la cycloïde ordinaire où le cercle générateur
de diamètre a roule sur le plan
horizontal à partir d’un point fixe (donné). Ce que l’on formule de la manière
suivante :
dy = dx√(x-(a-x) (2)
Toujours est-il que, comme l’a
écrit M. Blay : « Cette
solution, bien que différente dans son principe des deux précédentes, ne fait
pas intervenir, elle non plus, une quelconque conceptualisation différentielle
de la science du mouvement » [35].
La solution de l’Hospital. Informé
par Varignon du thème au centre des dissensions des plus grands savants de
l’époque, au cours d’une correspondance suivie entre eux, l’Hospital, une fois
le problème délivré des questions physiques et réduit à la « mathématique pure », se lance dans
la solution du problème en s’inspirant du thème de la funiculaire et de la
caténaire [36]. Dans son mémoire publié dans les Acta Eruditorum, inquiété aussi par quelques critiques de Johann
Bernoulli visant son modus operandi
l’Hospital n’expose que les résultats de son travail sans aucune démonstration.
Dans une première version de sa démonstration l’Hospital se contente de montrer
que la cycloïde, assimilée à un polygone à une infinité de côtés, vérifie la
règle de proportionnalité établie entre le sinus de l’angle de la tangente à la
courbe en un point et la verticale avec la vitesse de chute. Toujours est-il
qu’il faut faire quelques observations et préciser pour mieux comprendre une
telle solution. Soit AB=2r et r=1. La longueur de la
demi-circonférence est alors égale à L=pr=p=3,14. Se rappelant que la tangente en un point de la cycloïde
passe par l’extrémité du diamètre perpendiculaire à la droite sur laquelle
roule le cercle générateur et que la normale à la tangente au point de contact
passe par l’autre extrémité du diamètre du cercle générateur, on obtient, en
termes galiléens, que la vitesse que le corps acquiert durant sa chute est
directement proportionnelle à la racine carrée de la hauteur de chute. Sachant
que les côtés du polygone qui approchent la courbe sont infinitésimaux et donc
parcourus à une vitesse uniforme, on déduit que le corps va de B (voir Fig. 2) tournée de 90° à B’’ (de A en B), le long de la
courbe AB dans un temps minimum, si
cette courbe est une brachistochrone.
La courbe d’égale pression. En avril 1695, dans un supplément aux Acta Eruditorum, Johann Bernoulli propose de déterminer la nature
de la courbe d’égale pression (ou courbe centrifuge). Il s’agit de trouver,
dans un plan vertical, la courbe décrite par un corps qui descend sous l’action
de son poids propre alors qu’il est soumis à une pression en tous les points
générée par une force constante égale à son poids. La solution du problème fut
trouvée par Johann Bernoulli et communiquée à de l’Hospital après un long
échange de lettres durant les années 1695-96 ; finalement cette solution
fut mise au net par ce dernier et publiée en 1700 dans les Mémoires de l’Académie Royale des Sciences comme Solution d’un problème physico-mathématique.
Fig. 3a : Équilibre des forces; Fig. 3b : La courbe d’égale pression selon Johann Bernoulli
Le problème abordé par Johann
Bernoulli est le suivant (Fig. 3b) : déterminer «la courbe EFM, dans laquelle
le corps M descendant librement, et par
sa propre pesanteur, la presse dans toutes ses parties avec une force égale à
celle de son poids» ou, en utilisant à la manière de Huygens la développée HC de la courbe cherchée, « en sorte que le poids M attaché à l’extrémité d’un fil qui entoure
cette développée, décrive en descendant cette ligne courbe ; il faut que
dans chaque position du corps M, il
tende le fil développée MC avec la
même force que s’il étoit suspendu par ce fil» (Johann Bernoulli, 5 mars
1695). La solution du problème est beaucoup plus simple: il s’agit d’écrire que
la somme des forces agissant suivant la normale à la trajectoire est constante
et égale numériquement au poids. Il y a deux forces en jeu : la force
centrifuge et la composante normale au poids. Il suffit alors d’écrire que la
somme des intensités des deux forces est égale à celle du poids : mais –
ajoute l’Hospital – le corps arrivé au point M tend le fil MC avec
cette force centrifuge, augmentée de la partie de son poids qui agit sur le
point M de cette courbe par l’effet
de la pression suivant la perpendiculaire MS
du poids «absolu» - c’est-à-dire la quantité MR. La solution est sans difficulté lorsque l’on sait « par les Mechaniques» que si l’on suppose
que la partie constante MR de la
verticale PM prolongée précisément de
MR, exprime le poids absolu du corps M et que si nous traçons le segment RS perpendiculaire au segment MS qui coupe à angle droit la courbe au
point M, alors la droite MS exprime la quantité avec laquelle le
poids M agit sur le fil MC pour le tirer vers S. Le problème se réduit alors à
déterminer l’intensité de la force centrifuge «avec laquelle ce corps tend le fil MC» exercé par le corps en
mouvement, «afin de réduire cette
question à la pure géométrie» [37].
Le calcul de la force centrifuge dans le cas du mouvement circulaire [38]. Quelques années plus tard, en 1687,
Newton [39] donne la démonstration de ce problème dans le but de déterminer la
force centripète. « Les corps qui
parcourent uniformément différents cercles sont animés par des forces centripèdes
qui tendent au centre de ces cercles, et qui sont entr’elles comme les quarrés
des arcs décrits en temps égal, divisés par les rayons de ce cercle »
[40]. La solution de l’Hospital, qui se fie à plusieurs reprises à Johann
Bernoulli – déclarant ouvertement son « ignorance » de certaines
questions physiques – est la suivante: « … la force centrifuge feroit parcourir au corps M, un espace égal au quarré de l’arc MN appliquée au diamètre MK, dans le même instant que ce corps
parcoureroit l’arc MN ; puisque
par le moyen de cette force, le corps M se
trouvant en L au lieu d’être en N,
elle luy auroit fait parcourir la ligne NL» [41]. Cette affirmation
de l’Hospital appelle une remarque : ce résultat qui permet, connaissant
le rayon du cercle et la vitesse du mobile, d’exprimer le rapport d’une telle
force centrifuge à d’autres, ne satisfait pas totalement des conditions du
problème. Il est nécessaire, en fait, de mettre les deux forces en rapport avec
un même terme de comparaison qualifié par Johann Bernoulli, de poids absolu. On
comprend donc que l’Hospital désireux de trouver une solution correcte et
exhaustive du problème, se tourne immédiatement vers la recherche de la
solution d’un nouveau problème : déterminer la valeur du rapport des
intensités des forces centrifuges au poids (ou gravité). En résumé, il
s’agissait de comparer les espaces infiniment petits que, au même instant, la
force centrifuge et la gravité font parcourir au même corps. L’hypothèse
galiléenne du degré moyen [42] permet d’assimiler la vitesse constante du
mobile M qui se meut sur un cercle de
diamètre KM à celle générée par le
même corps au cours d’une chute d’une hauteur égale à PM (Fig. 4).
Fig. 4 –
Hypothèse galiléenne du «degré moyen».
Soit M le corps, t1
le temps de chute de la hauteur PM, t2 le temps de parcours de
l’arc MN, alors on a:
(t1/t2) = (2PM/MN) o (t12/t22) = (PM/(MN2/MN))
Donc la quantité (MN2)/(4PM) exprime l’espace que parcourerait le corps M au premier instant de la chute (durant
lequel il parcourt l’arc MN). Il est
donc possible de comparer « les
espaces que font parcourir ces deux forces (la force centrifuge et la
pesanteur) dans le même instant ». L’Hospital observe que l’on peut
considérer la gravité comme une force qui agit uniformément et sans
augmentation durant le premier instant de la chute à cause du caractère
infinitésimal du temps écoulé [43].
Si l’on pose que, n est l’intensité de la vitesse de M sur le cercle de diamètre MK et g l’accélération de la pesanteur, alors la solution de l’Hospital
conduit à la solution suivante. Appelons force centrifuge la quantité fc=((2PM/CM)•g), où g est la pesanteur (ou gravité), alors
on peut écrire que cette force vaut fc=(v2/R). Cette équation
représente l’expression de la force centrifuge dans le cas du mouvement
circulaire uniforme. À présent, si CM=R,
où R est le rayon de la
circonférence, et (2PM)=(v2/g), avec g égale à l’accélération de la pesanteur
on obtient le résultat cherché.
Dans le cas d’une
trajectoire quelconque, si MR
représente l’intensité de la pesanteur on obtient que la force centrifuge vaut fc=(2PM•MR)/MC, en chaque point de
la trajectoire ou en chaque instant du mouvement. Cette trajectoire [44] peut
être assimilée à une succession de petits arcs de cercle de rayon égal au rayon
de courbure et où les centres décrivent la développée HC de la courbe EFM.
Le problème de la courbe d’égale pression se réduit donc à
chercher une courbe EFM le long de
laquelle l’expression (2PM•MR)/MC+MS = MR est toujours vérifiée. Le problème se réduit
alors à un problème « de pure
géométrie ». En substituant à chaque « élément » géométrique
un symbole algébrique, par exemple MR=a, AP=x, PM=y, l’arce de courbe EFM=v, on obtient: MK=dx, Km=dy, Mm = dn (constant par
l’hypothèse de l’uniformité du mouvement). En substituant et en simplifiant on
peut écrire l’équation différentielle 2yddx+dydx=dvdy pour laquelle l’Hospital donne une solution [45]. Cette
solution fit d’ailleurs l’objet en 1708 d’une querelle au sein de l’ l’Académie Royale des Sciences de Paris
entre Parent et Saurin, due en substance à la difficulté de la nouvelle méthode
de calcul utilisée. En tout cas la solution de l’Hospital fut reprise et
développée des années plus tard (1710) par Varignon, avec rigueur de méthode,
élégance du calcul et caractère complet de la présentation des solutions.
Conclusions
L’évolution de la
recherche effectuée par les auteurs que nous avons cités se déroule
principalement en deux étapes : 1) ramener les questions les plus
importantes de la science du mouvement à des questions de «pure géométrie»; 2)
résoudre ces questions de «pure géométrie» à l’aide des nouveaux
« moyens » du calcul leibnizien. Cette évolution de la recherche
basée sur de nouveaux principes et de nouveaux instruments mathématiques,
contrairement à la finesse de certaines analyses de géométrie infinitésimale,
d’inspiration newtonienne, appliquée au mouvement - mais précisément exclusivement de géométrie
infinitésimale à cause de la réduction effectuée dans la première étape – ne
présente encore aucune conceptualisation différentielle spécifique de la
science du mouvement susceptible d’être soumise à des procédures algorithmiques
bien établies [46], puisque les grandes potentialités du calcul leibnizien sont
encore à exprimer. La question restait donc encore ouverte mais les
applications ultérieures au mouvement des projectiles dans un fluide élastique
aux nouveaux principes de l’hydrodynamique par Daniel Bernoulli et à la
mécanique des fluides en général, démontreront que les premières étapes de ce
chemin nouveau et complexe de la mathématisation du monde physique donneront
lieu à d’importantes modifications conceptuelles et linguistiques en Mécanique.
Bibliographie
[1] Kant E., Critica della ragion pura, a cura di
Pietro Chiodi; trad. di Pietro Chiodi; Utet, Torino, 1967
[2] Merleau-Ponty J.: Préface. In: Blay M., La naissance de la mécanique
analytique ; Puf, Paris, 1992, p. 3.
[3] Benvenuto,
E.: Natural philosophy, rational mechanics and practical engineering in
the work and life of Adhémar Jean Claude Barré de Saint-Venant, European
Journal of Mechanics, A/Solids, vol. 16, Special issue, 1997,
Gauthier-Villars, Paris, pp. 45-63. Vedi anche: Benvenuto, E.:
Adhémar-Jean-Claude Barré de Saint-Venant: the Man, the Scientist, the
Engineer, Atti dei convegni lincei, 140.
Giornata lincea. Il problema di de Saint-Venant: aspetti teorici e applicativi
(Roma, 6 marzo 1997), Accademia Nazionale dei Lincei, Roma, 1998, pp. 7-34.
[4] Leibniz,
G.-W.: Nova methodus pro maximis et minimis, itemque tangentibus, quae nec
Fractas nec Irrationales quantitates moratur, et singulare pro illis calculi
genus, Acta Eruditorum, Leipzig,
1864, pp. 467-473; Leibniz, G.-W.: De geometria recondita et analysi
indivisibilium infinitorum, Acta
Eruditorum, Leipzig, 1686, pp. 292-300.
[5] Gerhardt,
von G.I. Leibnizens mathematische
Schriften, Bd. 1-7; Halle, Berlin, 1849-63, V, p. 393.
[6] Blay, M., La naissance de la mécanique analytique;
Puf, Paris, 1992.
[7] Newton,
I., Philosophiae Naturalis Principia
Mathematicae; Londini, 1687.
[8] Huygens,
C., Horologium Oscillatorium; Paris,
1673.
[9] Galilei,
G., Discorsi e dimostrazioni matematiche
intorno a due nuove scienze …; Leyden, 1638.
[10] Blay, M., La
naissance de la mécanique analytique; Puf, Paris, 1992, p. 8.
[11] Fontenelle B, Le Bovier de, Elémens de la Géometrie de l’infini;
Paris, 1727.
[12] Leibniz, G.-W.: Nova Methodus pro maximis et minimis, op. cit., 1684.
[13] L'utilisation du terme “calcul” et “calcul intégré” et
a fait l'objet d'un long conflit entre les frères Jacques et Jean Bernoulli,
qui a eu lieu sur les pages de la.Acta
eruditorum.
[14] Fontenelle, B, Le Bovier de, in: Histoire de l’Académie Royale des Sciences avec les mémoires de
Mathématiques et de Physique pour la même année. Tirés des registres de cette
Académie. Année 1705 (1706), p. 141.
[15] Gerhardt, von G.I. Leibnizens
mathematische Schriften, Bd. 1-7; Halle, Berlin, 1849-63, V, pp. 222-223.
[16] Montucla, J. F., Histoire des Mathématiques; Paris, an
VII, II, p. 323 (Première édition du second volume: Paris, 1758).
[17] Gerhardt, von G.I. Leibnizens
mathematische Schriften, Bd. 1-7; Halle, Berlin, 1849-63, V, cap. III, § 1.
[18] Benvenuto, E., La
scienza delle costruzioni e il suo sviluppo storico; Sansoni, Firenze,
1981.
[19] Newton, I., Principes
Mathématiques de la philosophie Naturelle; Paris, 1756-1759. Traduction
française du marquis du Chastelet (nouvelle édition: Blanchard, Paris, 1966).
[20] Saladani, G., Compendio d’Analisi, Bologna, 1775, libro II, cap. XIII.
[21] Archives de l’Académie des Sciences de Paris. Registres
manuscrits des procès-verbaux des séances de l’Académie royale des Sciences des
Paris. Fol. 26, v°. Cfr aussi: Gerhardt, von G.I. Leibnizens mathematische Schriften, Bd. 1-7; Halle, Berlin,
1849-63, I, p. 276.
[22] Sur la
critique de M. Rolle au débat sur la infinilment
petits voir aussi: Blay, M., La naissance de la mécanique analytique;
Puf, Paris, 1992, pp. 42-62.
[23] Voir par
exemple les travaux de Jean Hudde (1633-1704).
[24] Le nom de
«courbe isochrone" a été introduite par Leibniz dans sa mémoire en 1689
intitulé:De Linea isochrona, in qua grave sive acceleratione descendit, et de
controversia cum Dn Abbate D.C., Acta
Eruditorum (1689), pp. 195-198.
[25] Huygens, C.:
Solution du problème proposé par M. L. dans les Nouvelles de la République des
Lettres du mois de septembre 1687, Oeuvres
complètes de Christiaan Huygens, 22 vol.; Société hollandaise des
sciences, La Haye, 1888-1950, IX, pp. 224-226.
[26] Leibniz, G.-W, op. cit., Acta
Eruditorum (1689), pp. 195-198.
[27] Jacobi Bernoulli Basileensisi, Opera, 2 vol.; Genève, 1744.
[28] Lectiones Mathematicae. Varia problemata
Physico-Mechanica, eorumque solutiones. Inventio Curvae descensus aequalibis. In: Johannis
Bernoulli ... Opera omnia tam antea sparsim edita, quam hactenus inedita,
vol. 4; Lausanne et Genève, 1742.
[29] Della
rettifica degli archi di una curva elastica, cfr. Jacobi Bernoulli Basileensisi, Opera, 2 vol.; Genève, 1744., vol.
I, p. 603.
[30] Voir à cet
égard Huygens, C., Horologium
Oscillatorium; Paris, 1673, 2e partie et Newton, I. Philosophiae Naturalis Principia Mathematicae; Londini, 1687,
Proposizione L.
[31] Une analyse approfondie de la mémoire des frères
Bernoulli et le marquis de L'Hospital est situé dans J. Peiffer, J., Le
problème de la brachystochrone à travers les relations de Jean I Bernoulli avec
L’Hôpital et Varignon, Studia Leibnitiana, XVII (1989), pp. 59-81.
[32] Newton, I., Philosophical Transactions, Genn. 1697, pp. 384-389. Cet essai a été réédité en Acta Eruditorum, Maggio 1697, pp.
223-224.
[33] Gerhardt,
von G.I. Leibnizens mathematische Schriften,
Bd. 1-7; Halle, Berlin, 1849-63, II, pp. 298-299.
[34] Huygens, C.,
Traité de la lumière; Leyden, 1690, p. 46.
[35] Blay, M., La naissance de la mécanique analytique;
Puf, Paris, 1992, p. 90.
[36] Voir le
problème d'une corde lourde, souple, inextensible et homogène, suspendu à deux
points fixes, le problème proposé par Jacques Bernoulli dans les mois de mai
1690 et réglé par Leibniz, Jean Bernoulli et Huygens. In: Benvenuto, E. op.
cit.; Sansoni, Firenze, 1981.
[37] Histoire de l’Académie Royale des Sciences avec les
Mémoires de Mathématiques et de Physique pour la même année. Tirés des
registres de cette Académie. Année 1700 (1703), p. 10.
[38] Cfr.
Huygens, C., Horologium Oscillatorium;
Paris, 1673 (Parte 5a), Théorème I, II, III a pag. 102. Voir aussi le mémoire
de 1659 intitulé «De vi centrifuga» publié
à titre posthume en 1703 Volder et Fullenius, in Oeuvres complètes de Christiaan Huygens, 22 vol.; Société
hollandaise des sciences, La Haye, 1888-1950. Opuscula Posthuma, XVI, pp. 260-267.
[39] Newton, I., Philosophiae Naturalis Principia
Mathematicae; Londini, 1687, prop. IV, Sec. II, Libro I.
[40] Newton, I., Principes Mathématiques de la philosophie
Naturelle; Paris, 1756-1759, p. 54, p. 56.
[41] L’Hospital, Marquis Guillaume de, Mém. Acad. Roy. Sci. Année 1700 (1703), p. 11.
[42] Galileo a
montré que si un corps M se déplace uniformément avec la vitesse qui acquiert une
chute de hauteur PM, il se rendra
dans le même temps une double ligne de PM. Voir Galilei, G., discours ..., op.
Théorème cit., 3e jour, I, Proposition I.
[43] L’Hospital,
Marquis Guillaume de, Mém. Acad. Roy. Sci. Année 1700 (1703), pp. 11-12.
[44] L’Hospital,
Marquis Guillaume de, Analyse des
Infiniment petits pour l’intelligence des lignes courbes, Paris,
1696, e anche Jean Bernoulli, Lectiones
Mathematicae. In: Opera omnia,
Lausanne et Gèneve, 1742.
[45] L’Hospital,
Marquis Guillaume de, Mém. Acad.
Roy. Sci. Année 1700 (1703), p. 13.
[46] Blay, M., La naissance de la mécanique analytique; Puf, Paris, 1992, p. 109.